아주 작은 Boltzmann 머신

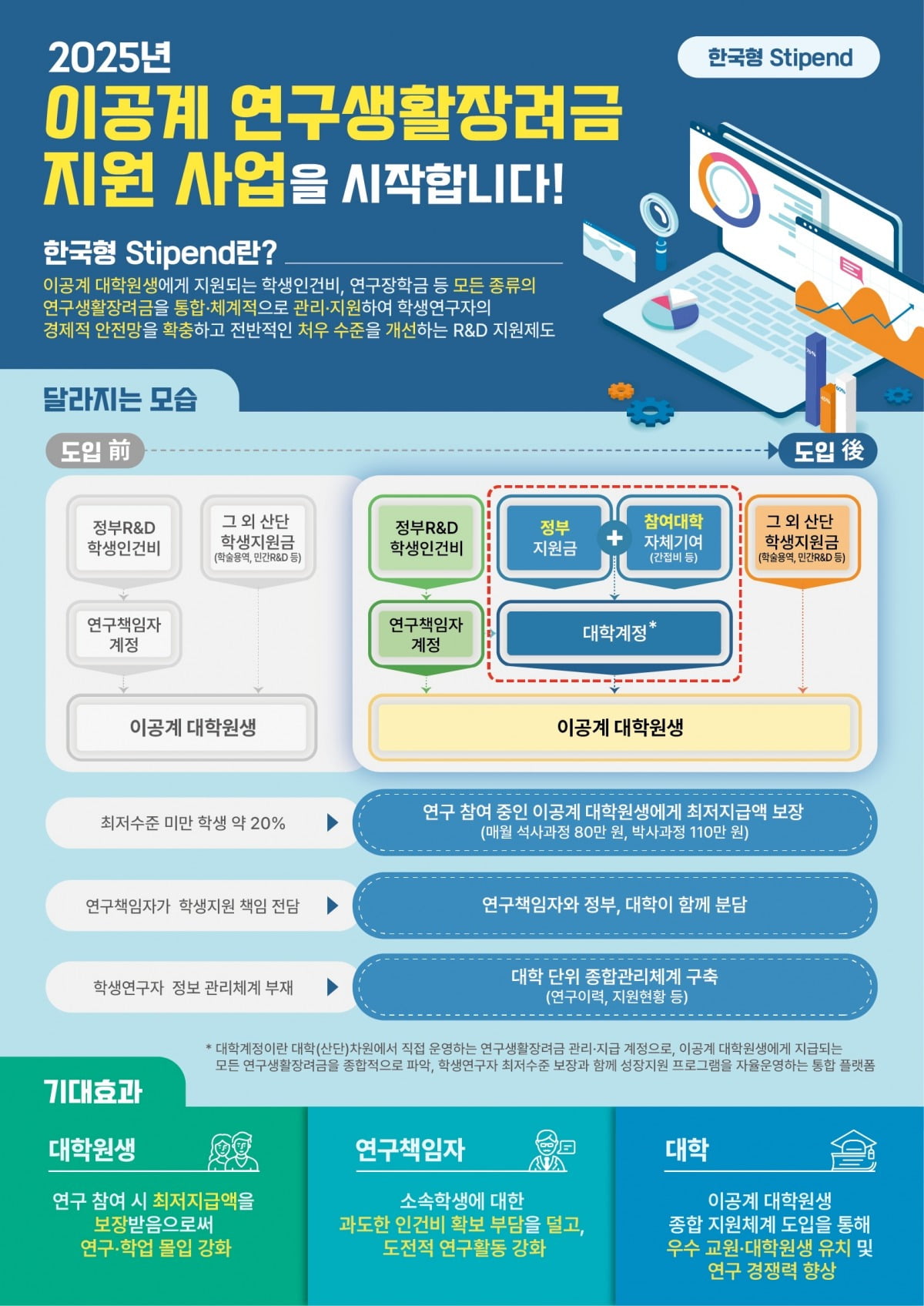
• Boltzmann 머신의 구조와 목적에 대한 간략한 소개임
• 에너지 함수와 확률 분포를 수식으로 정의함
• 가중치와 바이어스의 업데이트 규칙을 미분을 통해 유도함
• 긍정·부정 단계와 Gibbs 샘플링을 통한 모델 기댓값 근사 방법 설명임
• 최종적으로 대비 발산(Contrastive Divergence) 알고리듬을 전체적으로 정리함

Boltzmann 머신과 Contrastive Divergence 개념

• Boltzmann 머신에서는 입력층(visible layer)과 숨겨진층(hidden layer), 그리고 이를 연결하는 가중치 행렬과 두 층 각각의 바이어스 벡터를 가짐

에너지 함수와 확률분포

• 에너지 함수는 행렬 형태로 다음과 같이 정의됨

  E(v, h) = -ΣiΣj wij vi hj - Σi bi vi - Σj cj hj
  • v: 가시층 벡터, h: 숨겨진층 벡터, w: 가중치, b/c: 각 층 바이어스

• Boltzmann 머신의 결합 분포는

  P(v, h) = (1/Z) * exp(-E(v, h))
  • Z(분할 함수)는 확률분포를 정규화하는 역할임

로그 우도(log-likelihood) 및 미분

• 훈련 데이터의 우도를 최대화하여 학습 진행함

  log(P(v)) = log(Σh exp(-E(v, h))) - log(Z)

• 가중치 wij에 대한 로그 우도의 편미분은

  ∂(log P(v))/∂wij = <vi hj>데이터 - <vi hj>모델
  • < · >데이터: 실제 데이터에 대한 기댓값
  • < · >모델: 모델이 생성한 데이터에 대한 기댓값

가중치와 바이어스 학습 규칙

• 가중치와 바이어스는 다음과 같이 갱신함
  • Δwij = η(<vi hj>데이터 - <vi hj>모델)
  • Δbi = η(<vi>데이터 - <vi>모델)
  • Δcj = η(<hj>데이터 - <hj>모델)
  • η는 학습률

Contrastive Divergence 알고리듬

• 모델 기댓값 < · >모델은 직접 계산이 어려우므로 Gibbs 샘플링을 사용함
• Contrastive Divergence는 다음의 절차로 근사함
  1. 긍정 단계: 숨겨진층 h(0)을 P(h | v(0)=데이터)로부터 샘플링함
  2. 부정 단계: k번의 Gibbs 샘플링 반복
  • 번갈아가며 v(t+1) ~ P(v | h(t)), h(t+1) ~ P(h | v(t))으로 샘플링
• 업데이트 시각에서 데이터 기댓값과 모델 기댓값의 차이를 사용함
  • Δwij = η(<vi hj>데이터 - <vi hj>모델)
  • Δbi = η(<vi>데이터 - <vi>모델)
  • Δcj = η(<hj>데이터 - <hj>모델)

요약

• Boltzmann 머신의 학습 본질은 에너지 기반 모델로서 실제 데이터와 모델이 생성한 분포 간 기댓값 차이를 줄이기 위함임
• Contrastive Divergence는 이 차이의 근사를 빠르고 효율적으로 가능하게 하는 핵심 훈련법임
• Gibbs 샘플링을 통해 모델 분포와 실제 데이터를 연결하는 역할을 하며, 이 과정을 반복하여 Boltzmann 머신이 데이터를 잘 표현할 수 있도록 가중치와 바이어스를 업데이트함